
ESR1 Christin Bobe
Email: ; LinkedIn
I am working on the task “Modelling the landfill subsurface through integration of multi-sensor geophysical data”. This task represents the start of the ELFM value chain. It aims to deliver information on the amount of the landfilled material and on the value of the material for the further upcycling and processing techniques, the so-called exploration of the landfill. This exploration mainly consists of the application of non-invasive, electromagnetic geophysical techniques on the landfill sites and the processing of the data output. Do you have further questions? Do not hesitate to contact me via email: .
Problem statement & objectives
Once electromagnetic data is collected, these require processing in order to extract information about the subsurface contained. One standard approach to extract this information is inversion. The aim of inversions is to infer the unknown causes, the electrical conductivity and magnetic susceptibility distribution of the subsurface, for the observed data from the indirect measurements. The term inversion hereby refers to the reversed direction of causality as it is described in physical models. Using the physical model equations, parameters explaining the set of observed data are determined by inverse processing.
While the solution to a forward problem is almost always unique and stable, the solution to most geophysical inverse problems is mostly ill-posed, thus not unique nor stable. Non-uniqueness in the inverse problem means that there is not a unique set of parameters that explain the observed data equally well. Besides noise and other sources of error present in measurement data at all times, the sheer impossibility of collecting exhausting data sets causes this non-uniqueness to be a constant point of attention in geophysical data processing.
Throughout the years, different methods were used in geophysical data processing to deal with the omnipresent issue of non-uniqueness in the inverse solution. Two main inversion approaches are described in geophysical literature: deterministic and probabilistic inversion approaches. Here, it should be noted that deterministic approaches are more commonly used. One reason for this might be the large computational expense associated with the application of many probabilistic approaches. Yet, for many applications probabilistic inverse solutions become more frequently used. Probabilistic processing schemes have certain advantages over deterministic approaches that are desirable in many situations. First, the inherent non-uniqueness is captured in the probabilistic solution. And second, measurement errors other than noise can be included in the processing.
However, for large data sets that aim for complete areal coverage, for example from the electromagnetic exploration of landfills, probabilistic inversion is not standard. This might be explained by two main reasons. First, the forward model relating subsurface electrical conductivity (and magnetic susceptibility) and the measurement response is non-linear. For most applications, the inverse solutions therefore need to be computed numerically, running the forward model often hundred thousands of times. Second, the sheer size of data sets acquired in mobile configurations making data processing even more time-consuming.
The overall objective of this thesis is to introduce a framework for efficient probabilistic processing of large electromagnetic induction data sets. The aim of this processing hereby consists in the estimation of a probabilistic image of the electrical conductivity and magnetic susceptibility distribution in the subsurface.
The overarching objective can be split up in several sub-objectives relating to the general steps of probabilistic inversion:
- Objective 1: Sensitivity and depth of investigation estimation for FDEM data
- Objective 2: Efficient probabilistic inversion of FDEM data
- Objective 3: Simultaneous probabilistic calibration and inversion of FDEM data
- Objective 4: Joint inversion of FDEM and direct current resistivity data
Methods
For collection of electromagnetic data, we use a so-called multi-receiver small-loop FDEM device. For simulation of such data, we use the standard formulation as given by Ward and Hohmann (1988) as implemented by Hanssens (2019). For inverse modelling of this non-linear problem, we implement a Monte Carlo method, in particular the Kalman ensemble generator (KEG; Nowak (2009)).
Results obtained
The results are presented per objective:

Figure 1 - Part of the proposed measurement setup for simultaneous calibration and inversion of FDEM data
Objective 1: We present a novel characterization of geophysical measurement sensitivity and depth of investigation of geophysical data showing diffusive energy propagation in the subsurface. This approach is based upon the statistical analysis of the Monte Carlo ensemble statistics, in particular mean and variance of prior and forward response ensemble. We show that the covariance between prior and forward response is equal to differential sensitivity up to re-scaling (and sampling errors). As this measure is derived from the Monte Carlo ensemble only, no further computations of the forward model are necessary. The full results are explained in the corresponding article[1].
Objective 2: We introduced the KEG into geophysical inversion. The KEG provides a computationally efficient alternative to the standard Markov chain Monte Carlo inversion approaches. We show how the KEG can be used for the simultaneous estimation of electrical conductivity and magnetic susceptibility.
Objective 3: By extending the FDEM forward and inverse modelling by systematic error parameters, we are able to include an estimation for the latter in inverse modelling. A meaningful estimation, i.e. a calibration of the FDEM data, can be achieved when FDEM field measurements are performed on two heights (Figure 1) for each location. Results are presented in corresponding conference contribution and a submitted manuscript.
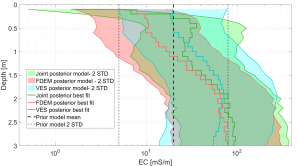
Figure 2 - Results for the posterior model of electrical conductivity for separate and joint inversion of FDEM and DC resistivity (VES) field data
Objective 4: We show how improved subsurface models of electrical conductivity can be achieved by joint inverse modelling of FDEM and direct current (DC) resistivity data. The improvement consists in (1) a reduced posterior model uncertainty, and (2) a best fit model that is (for the synthetic test cases) closer to the true model. For joint inversion of FDEM and DC resistivity field data, we demonstrate the straightforward application of the joint inversion, when the FDEM data use the scheme of simultaneous calibration and inversion as introduced (see results in Figure 2). All results are currently prepared in a manuscript to be submitted to peer-review.
Conclusion and outlook
The work conducted for this thesis provides a holistic framework for efficient probabilistic sensitivity analysis, calibration and inversion of FDEM data. Since the proposed framework is approximately a factor of ten to one hundred faster than Markov chain Monte Carlo (MCMC) methods, we believe that the interest in the presented methods will not be limited to the electromagnetic community.
For the investigation of strongly heterogeneous sites, such as landfills, the method can be considered beneficial to other types of inversion. First, in comparison to deterministic inversion, the KEG method gives a measure for uncertainty around the most probable result. Second, in comparison to MCMC, large data sets can be handled using the KEG.
[1] Bobe, C., Keller, K., and Van De Vijver (2020). Sensitivity and depth of investigation from Monte Carlo ensemble statistics. Submitted to Geophysical Prospecting.

